歓談
おはよー!ここ最近ずっと文字ばっかりの問題だったから、今日は図形の問題っをやってみよう。今日もかえでとぼたんと一緒にやっていこうね。


今日の目標
それではさっそく今日の目標の発表からやっていこー。今日の問題はこちら!
問 半径25cm、中心角72°の扇の半径が図のように5等分されている。赤色部分の面積はいくらかな?



例題
問題を解く前に、まずは公式の復習からやっていこー。円と扇それぞれに、長さと面積を求める式があるから合計4つの式が出てくるよ!おぼえている子もいるとおもうけどおさらいも兼ねてちょっとだけ付き合ってね。

★公式
円の面積=半径×半径×3.14
円周=直径×3.14
扇の面積=半径×半径×3.14×(中心角÷360)
扇の弧=直径×3.14×(中心角÷360)
多いようにみえるけど扇の公式は円の公式に(中心角÷360)をかけるだけだから、気負わずやっていこー。最初は公式をみながら問題を解こうね。

公式に慣れるために実際に問題を解いてみよう!4つあるよ。
(1)半径2cmの円の面積は□㎠
(2)直径 4cm、中心角90°の扇の弧は□cm
(3)直径□cmの円周は18.84cm
(4)半径6cm中心角□の扇の面積は18.84㎠

解答
(1) 半径×半径×3.14=円の面積
2 × 2 × 3.14=□
□=12.56(㎠)
(2) 直径×3.14×(中心角÷360)=扇の弧
4 × 3.14 × (90 ÷ 360)=□
□=3.14(cm)
(3) 直径×3.14=円周
□ × 3.14=18.84
□=18.84÷3.14=6(cm)
(4) 半径×半径×3.14×(中心角÷360)=扇の面積
6 × 6 × 3.14 × (□÷360) = 18.84
113.04 × (□÷360) = 18.84
□=18.84÷113.04×360=60°



①公式をかく
②わかっている数字を代入する
③もとめたいものを□とおく
この順番にやっていけばいいんだね。

練習問題
では実際に図形の面積を求めていこー。円や扇の面積がを求められらたらいろんな図形の面積を出せるんだよ!練習問題は2問あるから一緒にやってみようね。
ヒント:全体の面積から余分なものを引いてみよう!
(1)図1の半径が5cmの時、赤色の面積はいくらかな
(2)図2の正方形の1辺が10cmの時、青色の面積をもとめよう
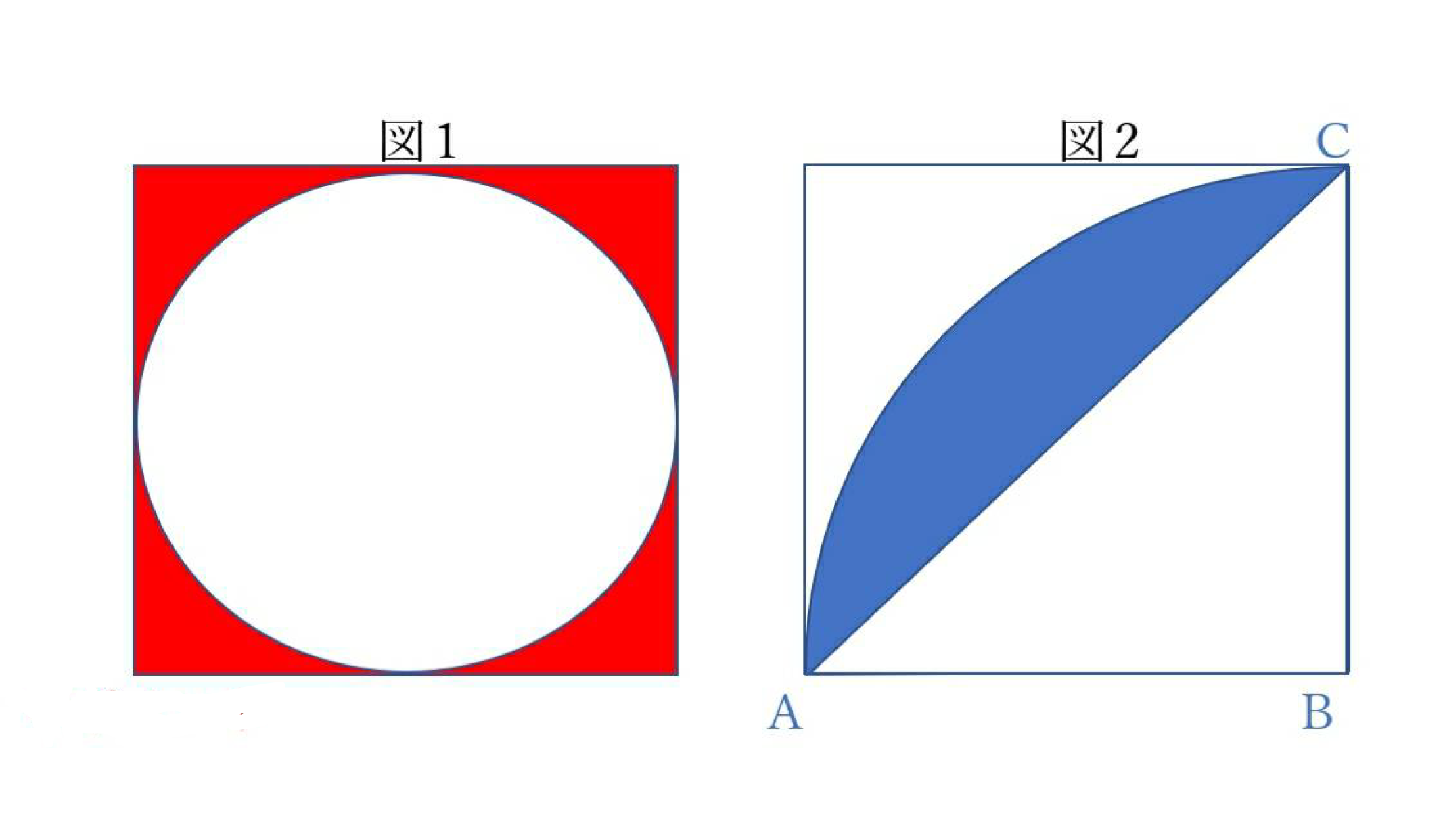

★ポイント
① 全体から余計なものをひいて求める
② ①の内容を計算する前に文字でかいておく
いまから私がやってみるね。
(1)
赤色の部分は正方形から円を引いて出せそうかな。
正方形 - 円 = 赤色の面積(←文字でかく!)
10×10-5×5×3.14=21.5(㎠)
正方形の辺と円の直径は同じ長さになることに注意しようね。
(2)
青色の部分は扇ABCから三角形ABCを引いて求めようね。
扇ABC - 三角形ABC = 青色の面積
10×10×3.14×(90÷360) - 10×10÷2 =28.5(㎠)
問題を解くときは知っていることをどんどん書いて、穴埋め問題に変えちゃおー!

今日の目標(解説)
最初にみた、Wi-Fi型の面積をもとめてみよー!求めたい面積をどうやって求めるのか、文字でかいてから計算していこうね。この問題の解説はぼたんにやってもらおうかな。
問 半径25cm、中心角72°の扇の半径が図のように5等分されている。赤色部分の面積はいくらかな(計算量が多いから電卓を使ってもいいよ!)


解説
一番上の赤色は①-②
真ん中の赤色は③-④
一番下の赤色は⑤
求める面積は赤色の面積全部だから
赤色の面積=①-②+③-④+⑤
扇の面積は半径×半径×3.14×(中心角÷360)だから
①=25×25×3.14×(72÷360)
②=20×20×3.14×(72÷360)
③=15×15×3.14×(72÷360)
④=10×10×3.14×(72÷360)
⑤=5×5×3.14×(72÷360)
①~⑤の値を上の式に代入して値を求めると235.5(㎠)
ふぅー…。がんばった!
6日目おわり



★ポイント
①円と扇の公式4つをおぼえる
②計算する前に計算内容を文字でかいておく
③むずかしい問題も穴埋め問題にかえてしまおう!
それじゃあまたねー!
