体積

歓談

こんにちは、今日は体積の求め方についてやっていくよ！昨日と違って今日は問題も計算もやさしめだからまったり読んでいってね。

みんな、こんにちは！今日は簡単ときいてやる気UP↑だよ。さくっとやって、やりたいことやろうね。

こんにちは。昨日は計算大変だったね。今日は体積の求め方について知っていこー。

今日の目標

やさしいといっても、この問題はちょっぴりむずかしいかも。できるかも！っておもったらぜひやってみてね。

問　図のように、三角柱から半径1cmの円柱をくりぬきました。体積が28.6㎤のとき、□はいくつかな？

あれれ、むずかしいや。どうしよー

大丈夫！ぱっと見むずかしいけど、これまで通り順番にやっていけばできるよ！例題からやっていこうね。

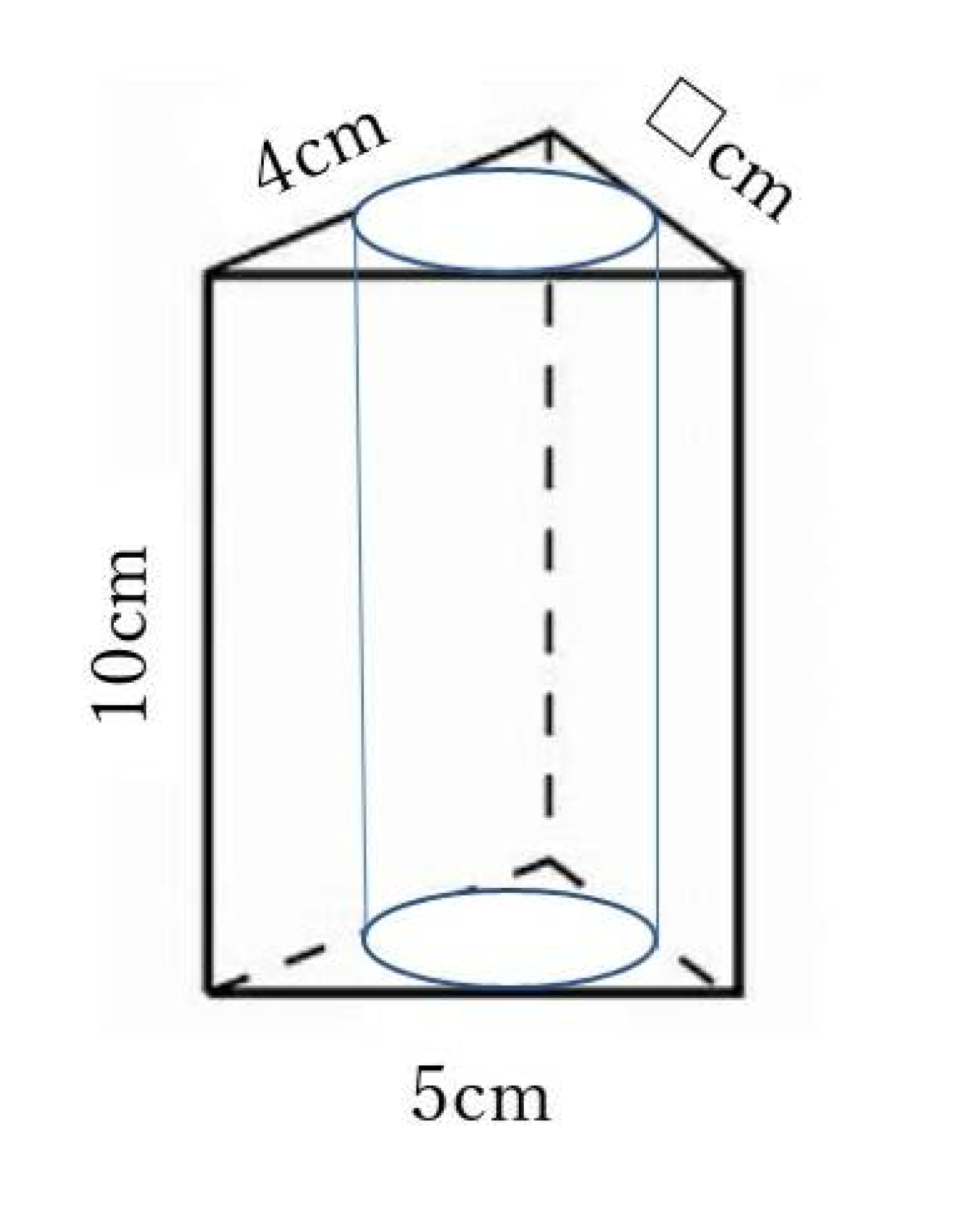
例題

まずは体積の求め方からはじめようね。今回の公式はひとつだけ！

今日使う公式はこれかな。

★ポイント
底面積×高さ＝体積

これだけでいいの？って思う子もいるとおもうけど、これだけだよ！あとは昨日とおなじく計算する前に公式をかいておこうね。それじゃあ例題いってみよー！

例題　次の図形の体積をもとめよう！

ふふ、できたよ！私が解説するね。

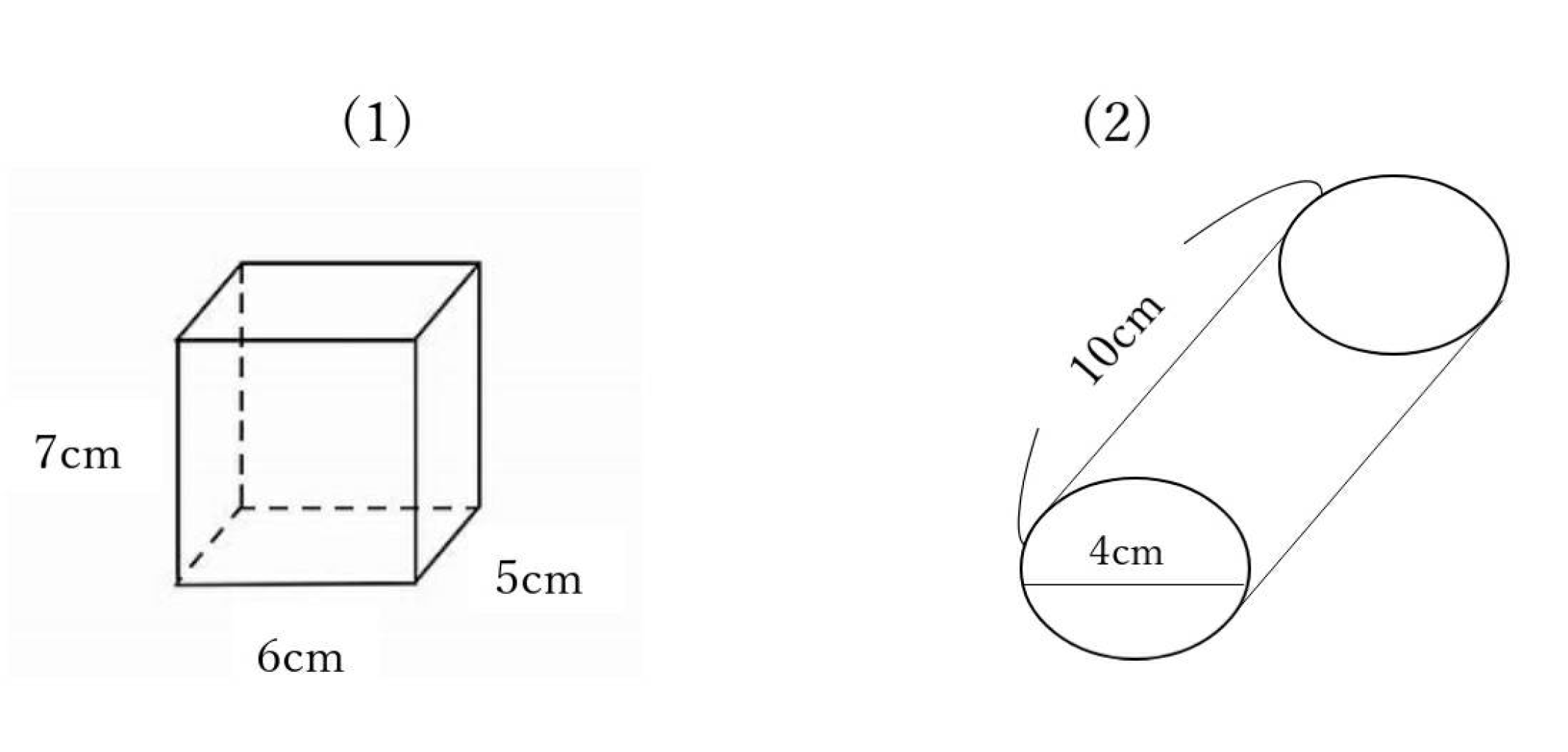
(1)
まずは公式をかいて、底面積×高さ＝体積
底面積=6×5=30㎠　高さ=7cmを代入すると
30×7=210㎤

(2)
上でかいたけどもう一回！底面積×高さ＝体積
底面積=2×２×3.14=12.56㎠　高10cmを代入して
12.56×10=125.6㎤

ばっちりできたよ！

やったねぼたん！
ここでひとつ大事なことを説明するね。(2)の円柱に注目すると、底面積を円にしたことに違和感はないとおもうの。

「底面積だからといって下の面とは限らない」このことは頭にいれておこうね。じゃあ練習問題に進んでいこー。

練習問題

次にやる問題は体積がわかっているときの、図形の辺の長さを求める問題だよ。このあたりから、公式をかかないと計算ミスをしやすくなるから気をつけよう。

練習問題
(1)三角柱の体積が120㎤のとき高さは何cmかな。
(2)円柱の体積が251.2㎤のとき高さは何cmかな。(高さを□とおいてみようね)

この問題は私が解説するね。公式をかいて、落ち着いて計算すれば大丈夫だからていねいにやっていこー

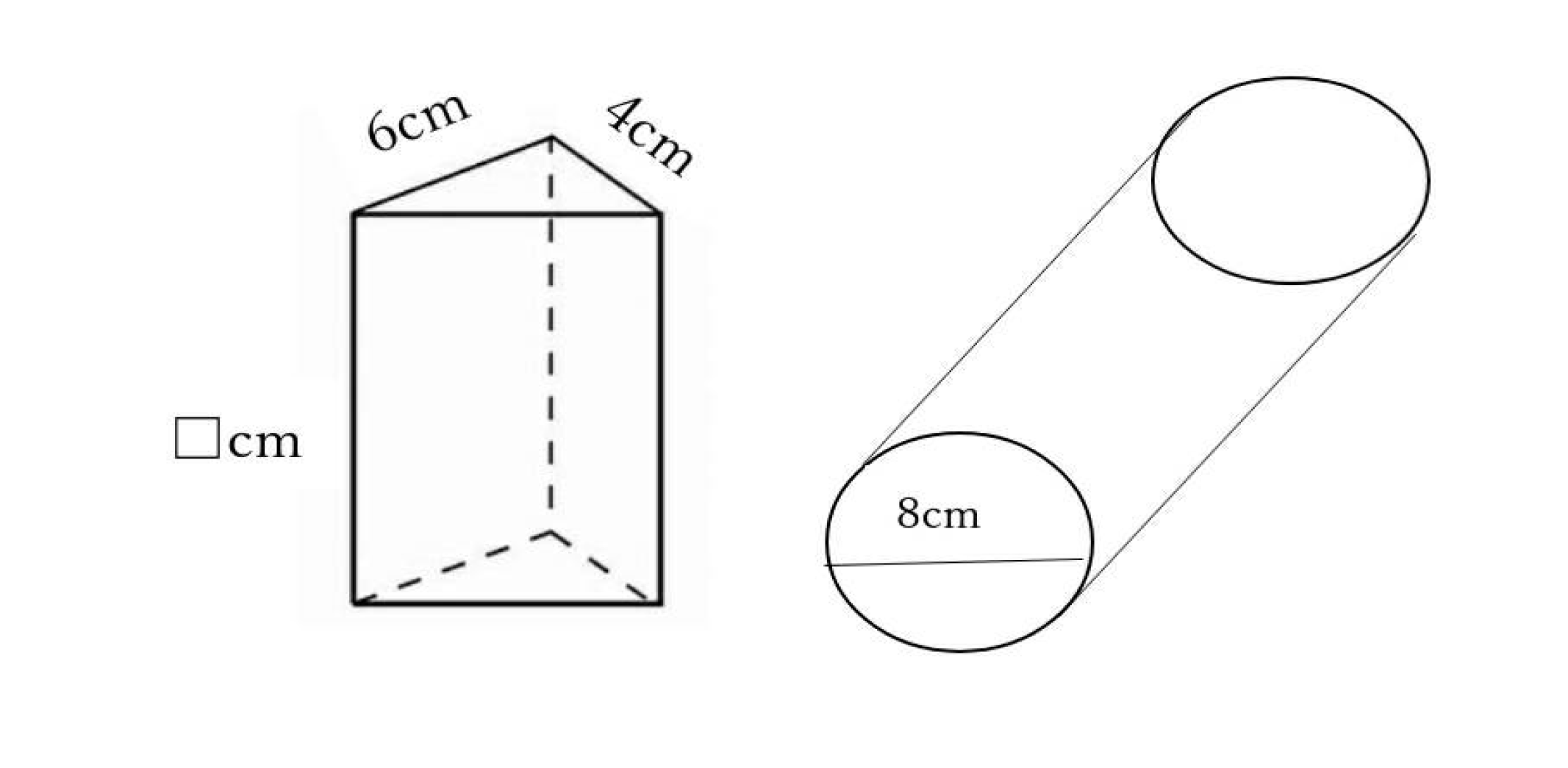
(1)まずは公式をかいて、わからないところは□にするよ！
底面積×高さ＝体積

底面積=6×4÷2＝12㎠
高さ＝□cm
体積=120㎤

それぞれ公式に代入すると
12×□＝120
□＝120÷12＝10cm

(2)おなじくまずは公式！底面積×高さ＝体積

底面積=4×4×3.14＝50.24㎠
高さ＝□cm
体積=251.2㎤

それぞれ公式に代入して
50.24×□＝251.2
□＝251.2÷50.24＝5cm

みんなできたかな。細かくかくと

①公式をかく
②わかっている数字を書き出す
③求めたい値を□とく
④公式に代入して計算

この流れだよ、ゆっくりおぼえていこうね。

私はいまのところ大丈夫だよ。このまま今日の目標もやっちゃえそー！

今日の目標(解説)

今日の目標もこの調子でやってみようね。かえでが練習問題の解説で言ってる通りにかいていくとできるはず！少しややこしいけど一緒にやってみよう。

問　三角柱から半径1cmの円柱をくりぬきました。体積が28.6㎤のとき、□はいくつかな？

いまの私ならできる気がする！がんばってやってみるね。

まずは公式をかいて、底面積×高さ＝体積

底面積＝□㎠　わからないときは□にしちゃう！
高さ＝10cm
体積…これは出せるよ！
三角柱―円柱＝28.6㎤　円柱の体積は1×1×3.14×10＝31.4㎤
三角柱の体積＝28.6㎤＋31.4㎤＝60㎤

それぞれ公式に代入すると
□×10＝60
□＝60÷10＝6㎠

底面積は三角形の面積なので
底辺×高さ÷2＝底面積
4×□÷2＝6
□＝3cm

ふふふ、これで私も体積マスター！

7日目おわり

今日もたくさん勉強したね。みんなもぼたんもお疲れ様！

そうだね、今日もよくがんばった！かえでもおつかれ～。今日は立体の体積だったけど明日はなんだろ…？

明日は立体の表面積の求め方についてやっていこうね。今日はもうあそぼー！最後に今日やったことをメモしとくね

★ポイント
①公式をかく
②わかっている数字を書き出す
③求めたい値を□とく
④公式に代入して計算

それじゃあぼたん、あそぼー。みんなもまた明日ね。ばいばーい。

うん、あそぼー！それじゃあまたねー。