歓談
こんにちは!今日は昨日に続いて立体図形についてやっていくよ。昨日は体積の求め方について勉強したけど、今日は表面積だね。苦手とする子も多いところだけど大丈夫だよ、一緒に気楽にやっていこうね。



今日の目標
今日の目標はこれだよ。なんか見たことあるなぁって思った子は鋭い!昨日と図形は同じだね。ややこしそうだけど大丈夫だよ、例題から順番にやっていこうね。
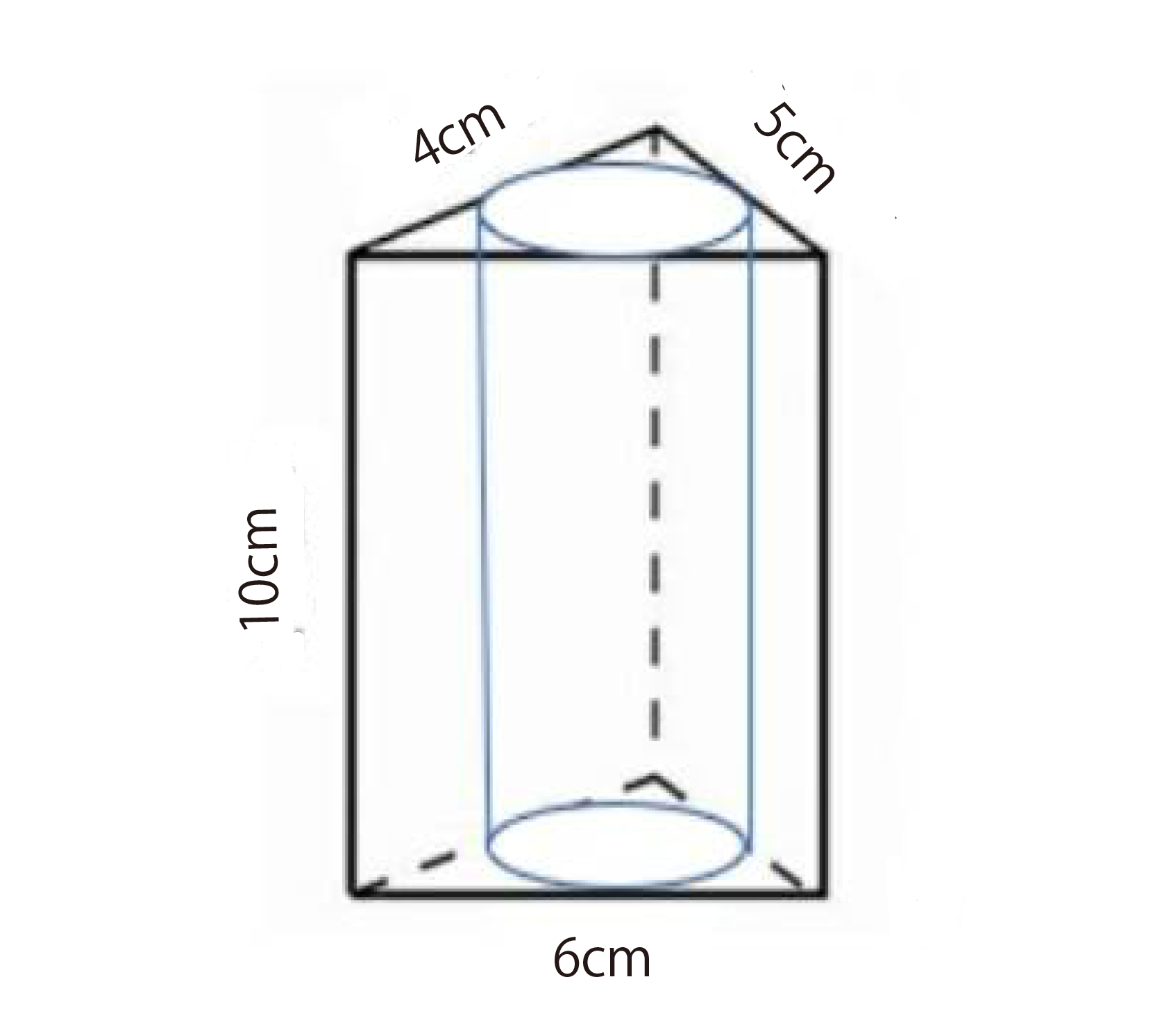
三角柱から半径1cmの円柱をくり抜いたとき、残った立体の表面積はいくらかな?


例題
「どこを計算したかわからなくなる」、「何回やっても計算が合わない」とよく言われる表面積の問題だけど、ミスをなくす鉄則があるよ!なので、まずは表面積を求めるときの計算の仕方について説明するね。

空間把握がかなり優れている子は頭の中で計算できちゃうかもだけど、私みたいにどこを計算しているのかごっちゃになっちゃう子にはとってもおすすめだよ!
★ポイント
●(前、後ろ),(右、左),(上、下),+覗き込みなどにわけて考える。(円柱や三角柱だと求める箇所は少なるよ!)
●前後、左右、上下は同じ面積になることが多い。(どちらかの面積が求まると2倍してあげたら両面の面積が出せるよ!)
●覗き込みっていうのは、外からはみえない、くり抜かれている部分の側面積のことだよ!
すこし手間にみえるかもしれないけど、求める箇所を最初に文字でかいてしまうのが良いよ!
まずはかえでのやりかたに慣れるためにいくつか例題をやってみようね。
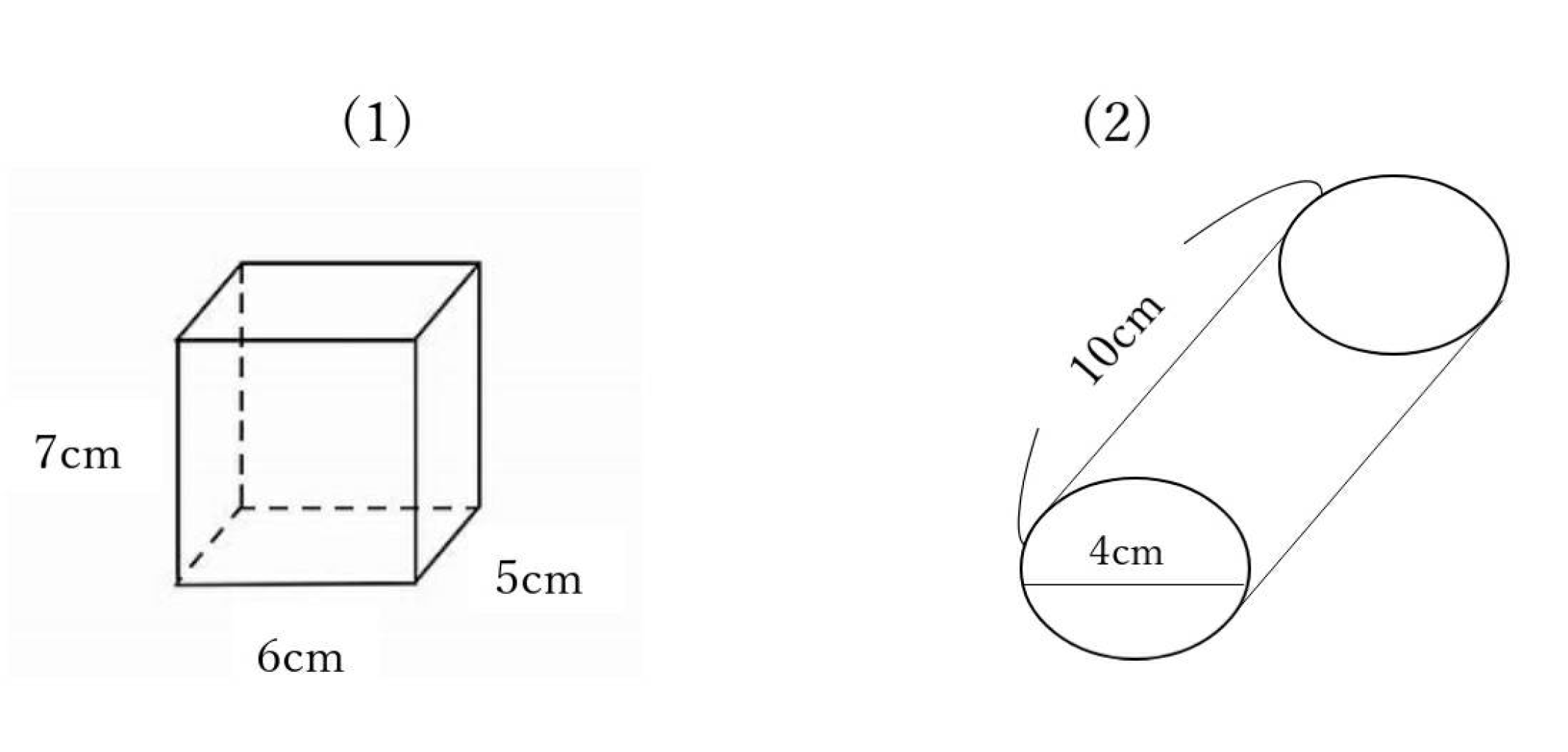
例題 次の2つの立体図形の表面積を求めてみよう!

解説
(1)
前後 6×7=42 42×2=84㎠
左右 7×5=35 35×2=70㎠
上下 5×6=30 30×2=60㎠
全部足すと、84+70+60=214㎠
(2)
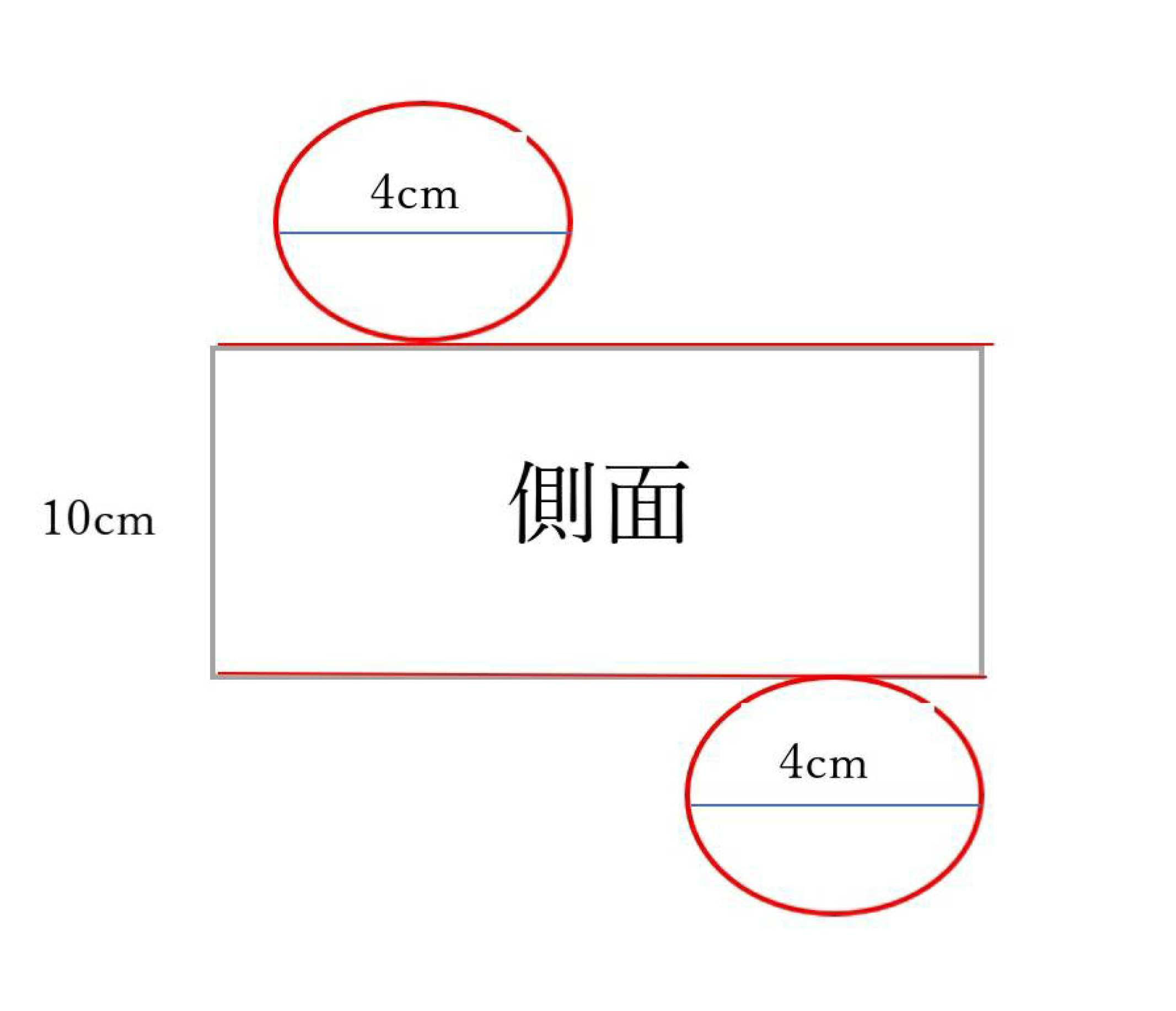
円柱の時は底面と側面にわけようね。側面の求めかたが難しければ、展開図をかいてみよう!

面の横の長さは底面の円周と同じに長さになるよ!
底面積 2×2×3.14=12.56 12.56×2=25.12㎠
側面積 10×4×3.14=125.6㎠ (側面は1つしかないから2倍しないよ)
全部足すと、125.6+25.12=150.72㎠
どうかな?(2)側面積で迷った子も多いとおもうけど、「展開図の横の長さ=底面の円周」がわかったら大丈夫だよ!


練習問題
今回の練習問題はひとつだけなので、よかったらみんなも試しに解いてみてね。今回も円柱の側面積を求めるから、難しかったら例題の解答を参考にしてもらえたら良いかも!
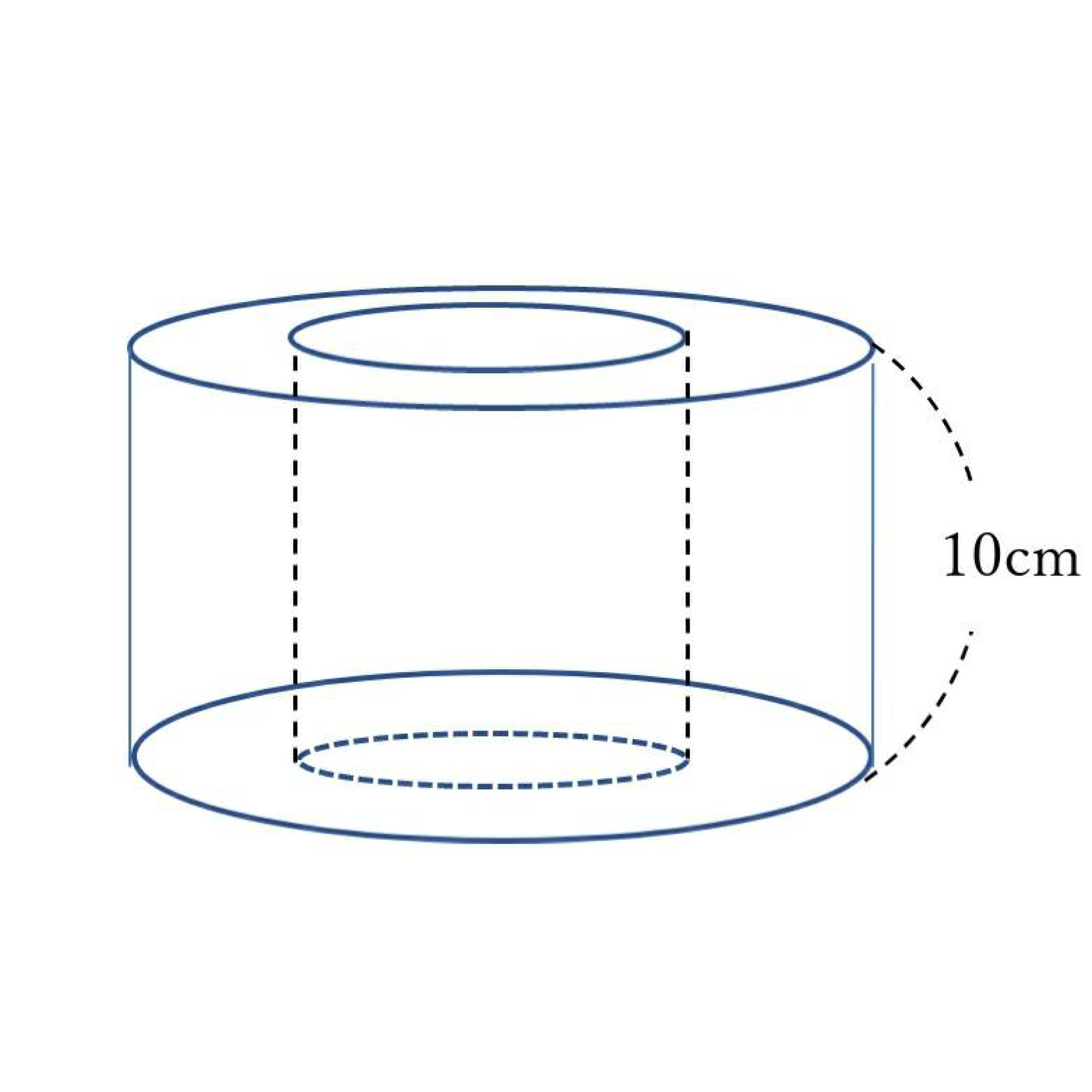
練習問題 半径4cmの円柱から半径2cmの円柱をくり抜いたバームクーヘン型の表面積はいくらかな?

解答
底面積(上下)、側面積、覗き込み、求めるのはこの3つ!
底面積(上下) (4×4×3.14-2×2×3.14)×2=37.68㎠
側面積 10×(4×2×3.14)=251.2㎠
縦 × 横(円周) (例題と同じだよ!)
覗き込み…今回は円柱がくり抜かれているから、求めるのは半径2cm高さ10cmの円柱の側面積とおなじかな。
10×(2×2×3.14)=125.6㎠
求めた3つの数字を足して37.68+251.2+125.6=414.48㎠
求めるものが多いけど、ばらして一個ずつ求めてあげたら大丈夫かも。今日はもうこの問題だけでおなかいっぱいだよー。

今日の目標(解説)
それでは今日ラストの問題をやってみようね。例題、練習問題とおなじようやっていけばできると思うよ!
問 三角柱から半径1cmの円柱をくり抜いた。残った立体の表面積はいくらかな?


解説
まず求める箇所は上下、前、左、右、覗き込みの5つだね。
上下 4×5÷2-1×1×3.14=6.86 6.86×2=13.72㎠
前 6×10=60㎠
左 4×10=40㎠
右 5×10=50㎠
覗き込み 10×(1×2×3.14)=62.8㎠
全部足して13.72+60+40+50+62.8=226.52㎠
みんなできたかな。1番むずかしいのは覗き込みのところだとおもうけど、くり抜かれているのが「半径1㎝、高さ10㎝の円柱」だから、その側面積を求めてあげたらおっけーだよ!
8日目おわり




★ポイント
●(前、後ろ),(右、左),(上、下),+覗き込みにわけて考える!
●計算するまえに求める箇所を文字でかいておく
●円柱の側面積は底面の円周×高さで求まる(展開図をかくのも◎)
こんなかんじかな。それじゃあまたね、明日も一緒にやってくれると嬉しいな。
