歓談
こんにちは、今日は錐の体積・表面積についてやっていくよ。昨日の容積よりは少しだけ楽だから安心してね。今日もかえでとぼたんとまったりゆったり進めていこう!





今日の目標
今回の問題はかなりシンプルだけど、逆に情報が少ないから難しいかも!
問題 ある円錐において、底面の半径は2cm、母線は10㎝です。この円錐の表面積は?
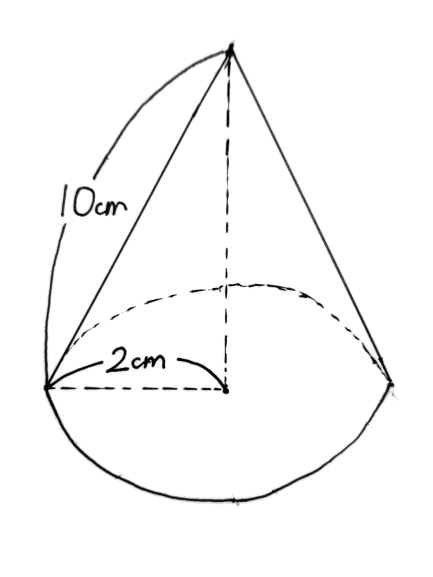


例題
それでは最初に錘の体積の求め方からやっていこー。
公式は
底面積×高さ÷3=体積
さきっぽがとがっている分、直方体や柱の体積よりも小さくなっているから÷3がくっついてくるよ。まずは公式に慣れるためにもいくつか問題をやってみようね。
例題 (1)円錐の体積を求めてみよう
(2)四角錐の体積が64㎤のとき、高さはいくらかな
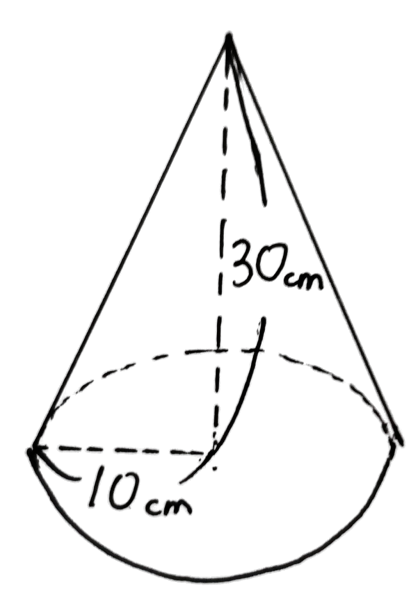


(1)
底面積×高さ÷3=体積
底面積=10×10×3.14
高さ=30㎝
これらを公式に代入して計算すると
10×10×3.14×30÷3=3140㎤
(2)
底面積×高さ÷3=体積
底面積=4×4=16㎠
高さ=□㎝ (求めたいものは□とおこうね!)
公式に代入して計算すると
16×□÷3=64
□=64×3÷16=12㎝
(2)の□を求める計算で迷ったら1日目の計算のところを見てみてね!


練習問題
それでは今日のメインテーマ、円錐の表面積についてやっていこー!
かえでに説明してもらうから、まずはみんなも一緒に読み進めていこうね。

まず円錐の表面積は底面積と側面積の2つからできてるよ。そのうち底面積は円の面積だから求めるのはむずかしくないとおもう!ここでは特に側面積について詳しくやっていくね。
円錐の側面積を考えるとき、必ずかくのが展開図なの。実際にかくね。
側面積…扇型の部分
底面積…円の部分
扇の半径…円錐の母線
いきなりたくさんの情報がはいってきてるから、指さししながら確認していこう!イメージがつかみにくかったら、実際に円錐をつくって展開してみるのもいいかも。
続けて説明していくね。側面積=扇の面積だとすると、「扇の半径はわかっているけど中心角はどうなるの?」ってなるとおもうけど、ここで新しい公式!
公式
中心角×母線=底面の半径×360
この式はすっごく大事だから何回もかくか、叫んで覚えてしまお!なんでこの式が成り立つのか気になる子は、最後に説明するから見てみてね。

中心角×母線=底面の半径×360
だよ~!!!

では、練習問題をやってみましょう。
問題
(1)半径4㎝、母線8㎝のとき中心角は何度?
(2)母線12㎝、中心角270°のとき半径の大きさは?
(3)半径3㎝、中心角60°のとき母線の大きさは?

(1)
まずは公式をかいておこ( ..)φ
中心角×母線=半径×360
半径4㎝、母線8㎝、中心角を□にして代入すると
□×8=4×360
□=360×4÷8=180°
(2)
とりあえず公式!
中心角×母線=半径×360°
母線12㎝、中心角270°、半径を□にして代入すると
270×12=□×360
□=270×12÷360=9㎝
(3)
最後もやっぱり公式から!
中心角×母線=半径×360
半径3㎝、中心角60°、母線を□として代入すると
60×□=3×360
□=360×3÷60=18㎝
できた!これでどの大きさを聞かれても全部答えられるようになったよ!
今日の目標(解説)
最後に今日の目標をやっておわりにしよー!練習問題でやった公式と、円や扇の面積(6日目参照)の求め方がわかればできるから一緒にやってみようね。必ず展開図をかくことを忘れずに!
問題 ある円錐において、底面の半径は2cm、母線は10㎝です。この円錐の表面積はいくらかな


解説)
まずは公式をかいてっと。先に展開図でももちろんいいよ!
中心角×母線=半径×360
半径2㎝、母線10㎝、中心角を□とおいて代入すると
□×10=2×360
□=2×360÷10=72°
円錐の表面積は底面積と側面積から求められるから
それらを求めてあげたらOK!
底面積 半径2㎝の円
側面積 半径(=母線)10㎝、中心角72°の扇
底面積 2×2×3.14=12.56㎠
側面積 10×10×3.14×(72÷360)=62.8㎠
12.56+62.8=75.36㎠
どうかな、みんなできたかな?展開図をかいて、そこに公式から得られた情報を書き込んでいくと答えがみえてくるよ!
10日目終わり



★ポイント
●錐の体積 底面積×高さ÷3=体積
●円錐の表面積 中心角×母線=半径×360
●円錐の表面積は展開図をかく
この3つだったね。今日全部おぼえなくて大丈夫だからゆっくり解き方をおぼえていこう!

そういえば、「心角×母線=半径×360」ってどうやって導くんだろ?

円錐を展開図にすると、扇と円の2つからできていることがわかるんだったね。この時、扇の弧と円周がおなじ長さになっているの。
扇の弧=母線×2×3.14×中心角÷360
円周 =半径×2×3.14
扇の弧=円周なので
母線×2×3.14×中心角÷360=半径×2×3.14
ここで両辺を2×3.14でわると
母線×中心角÷360=半径
両辺に360をかけてあげて
母線×中心角=半径×360
文字でみるとごちゃごちゃするから、どんどん紙にかいて確かめてみてね!


