歓談
こんにちは、今日と明日は相似についてやっていくよ!文章問題が続いてたから久しぶりの図形だね。だけど、文章問題でやってきた比がここでも活きてくるから繋がってる部分もあるんだ。ということで図形の中でも重要な分野、相似についてやっていこー!

20日間一緒にがんばってきたみんなにも1日のどこかで算数の勉強をする習慣がついてきてるかも!これからも無理せずがんばろうね。


ではでは今日の内容にはいっていこっか。今日は相似についてやっていこうね。


すこし説明が長いけど、その分問題は少なくなってるよ!
今日の目標
今日の目標はこれだよ。図形の問題だから問題文は今までと違ってかなり短いかな。
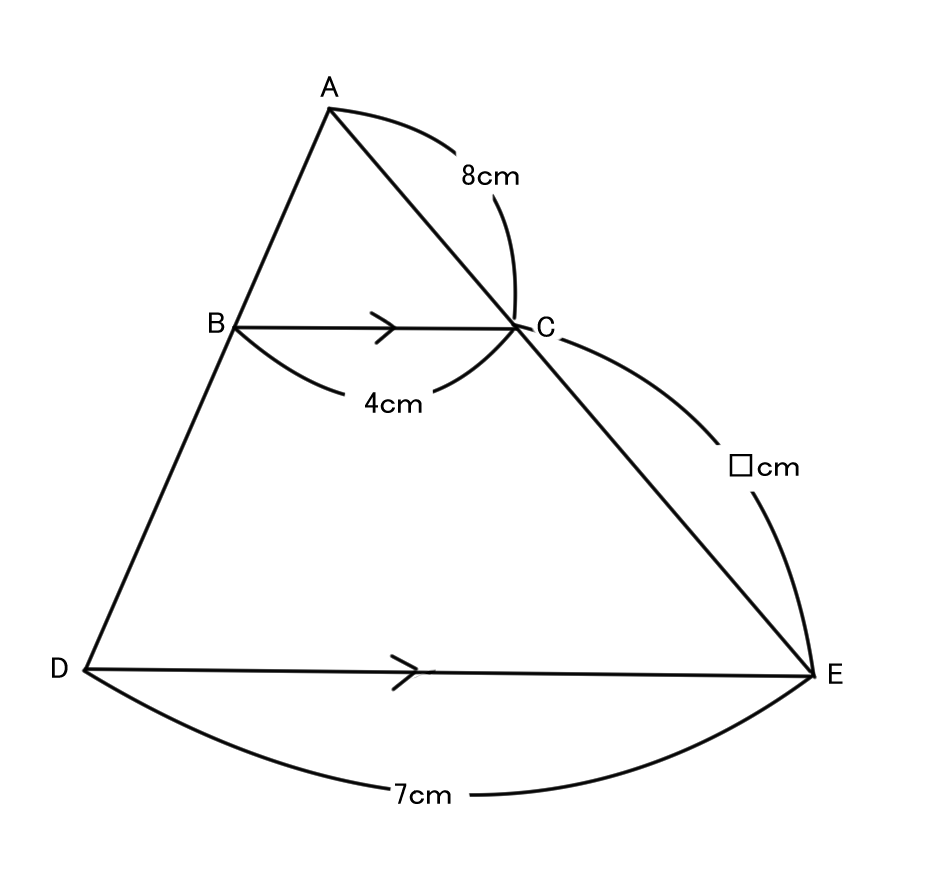
問題
図の□の長さを求めてみよう。



例題
それでは例題をやっていきましょう。でもその前に相似の問題をやる上で大事なポイントを紹介するよ。ということでかえでに教えてもらいましょう。

まず相似の問題は三角形の相似しか出ないなので、今回は三角形の相似について話していくよ。
●三角形の相似条件
異なる2つの三角形がある場合に2つの角度の大きさが同じなら、それらの三角形は相似だよ。
(2つの角度が同じってことは、残る1つの角度も同じになるから、結局は三角形の3つの角度全部が同じになっていることを示しているよ。)
●よく出てくる相似の形
上の条件は読んだだけじゃわかりにくいから、実際によくある図形を用いて説明するよ!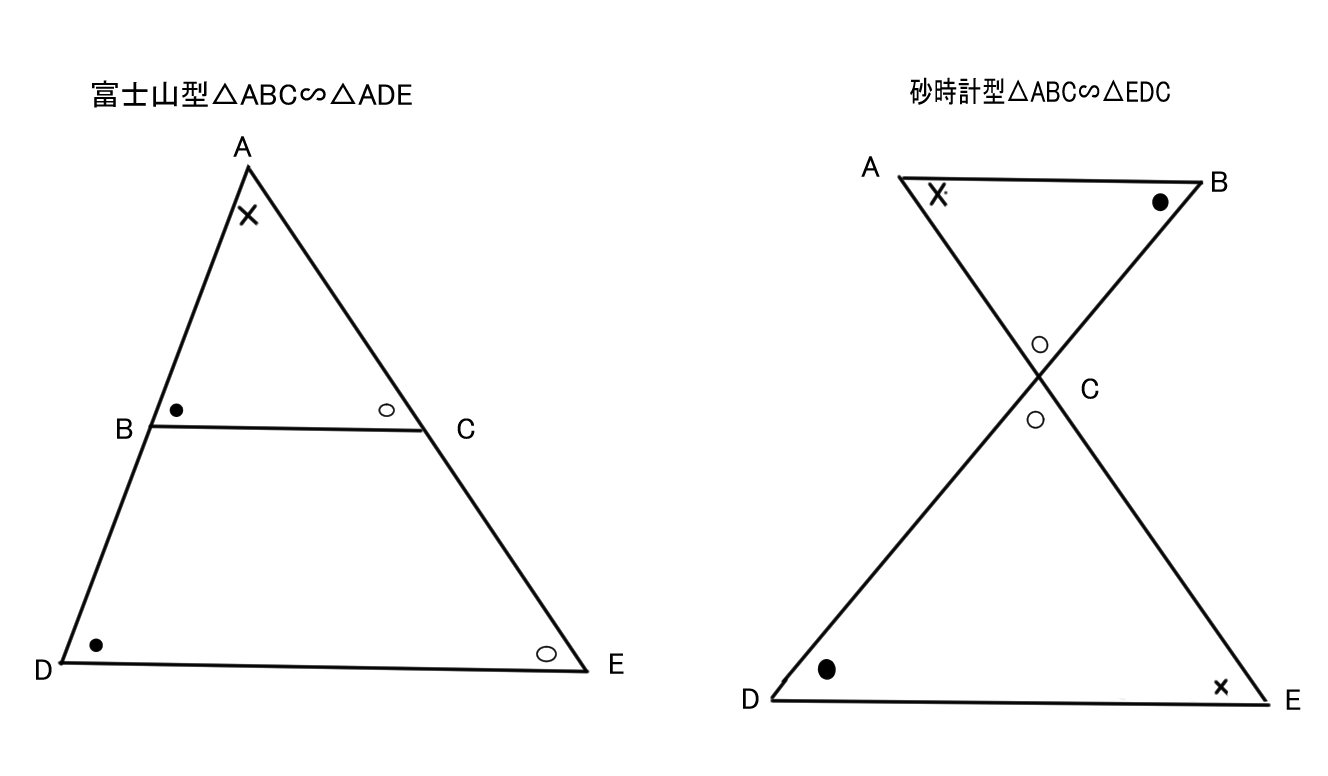
富士山型と砂時計型は、三角形の相似の問題の中でも特に多いから、この形をみたら相似を疑おうね。
●相似比
実際に問題を解くときに1番使うのが相似比だよ。
相似比とは拡大・縮小するときの割合を比で表したもののこと!
例えばこの図形でいうと相似比は4:3になるよ。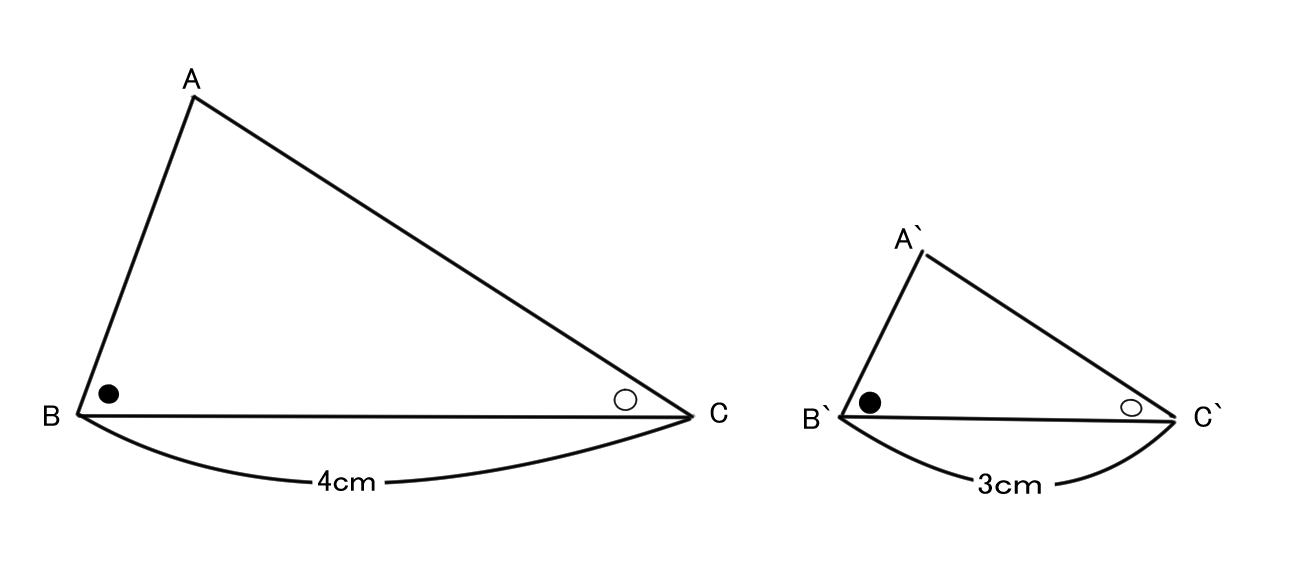
★ポイント(手順)
1.相似比をみつける
2.図に比をかきこむ
3.長さを求める
それでは例題で手順をためしていこうね。
例題
次の図形の□の値を求めてみよう。

解説)
まず△ABCと△DEFは相似
このことを△ABC∽△DEFとかくよ(∽:相似マーク)
1.相似比を求める
BC:EF=2:3
2.図に比をかきこむ
相似比が2:3だからAB:DEも②:③
3.長さを求める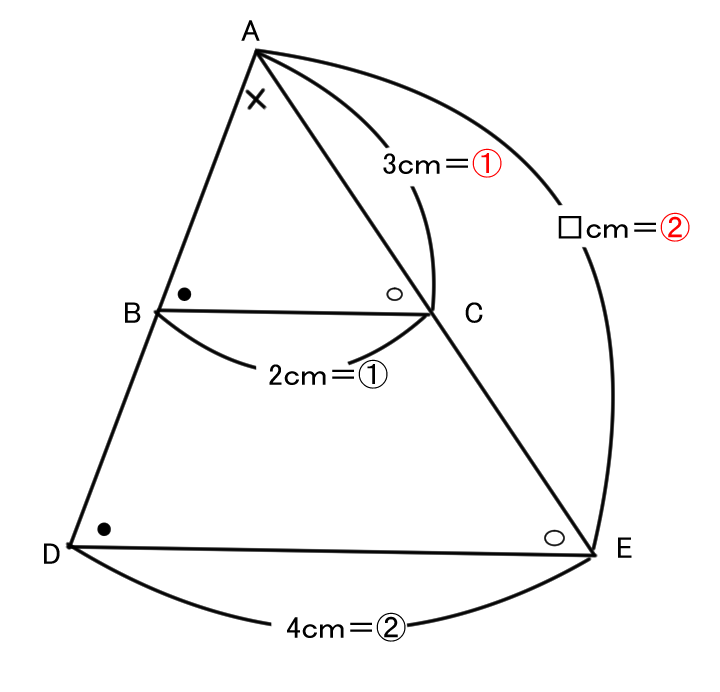
AB=②=4cm
①=4÷②=2cm
□=DE=③=2×3=6cm
相似比っていうのは拡大・縮小の割合だから、1組の辺の比さえわかってしまえば他の組の辺も同じだよ!


次は相似比を絶対間違えない探し方について説明していくね!
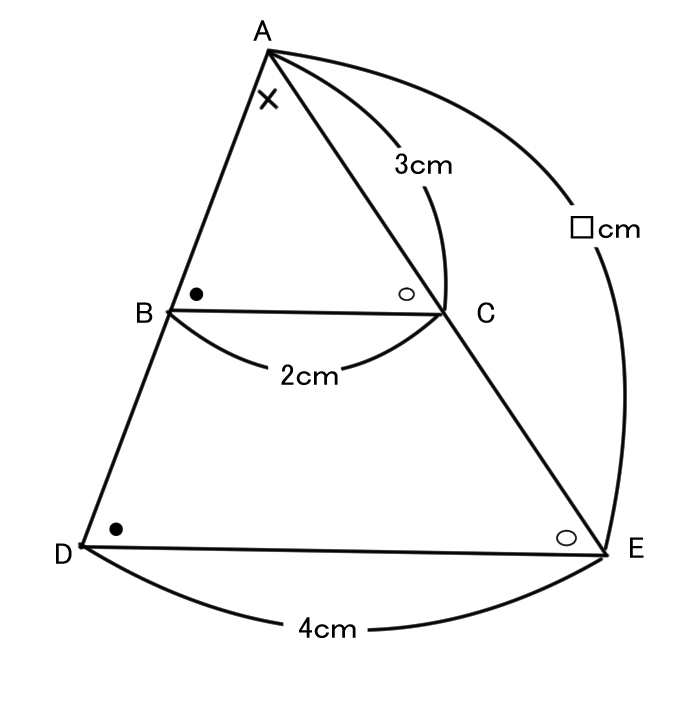
練習問題(相似比の見つけ方!)
ここでは相似比の見つけ方をメインにやっていくよ。まずは説明をきいてみてね!

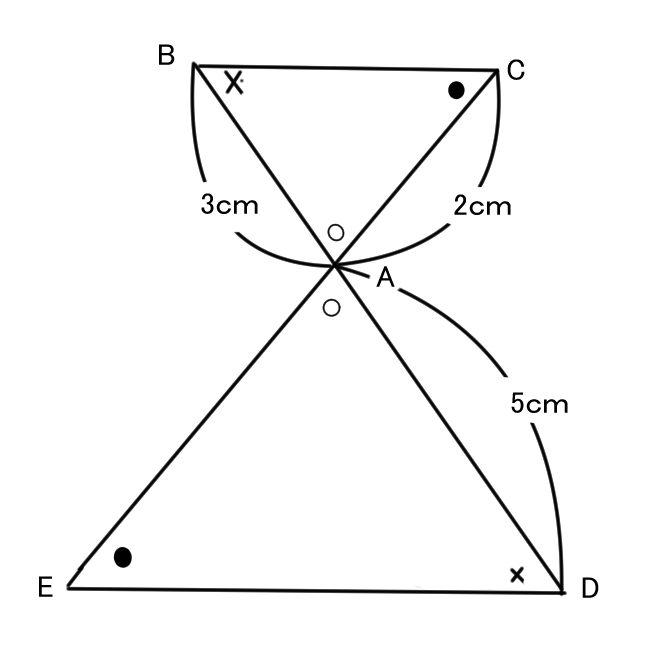
この図(砂時計型)をつかって説明していくよ。
まず△ABC∽△ADEだね。
でも、△ABC∽△AEDとは普通かかないよ、その理由と相似比を間違えないように求める方法はすごく関係しているからぜひ読んでいってね!


ABCとADEの並び順にはちゃんとした法則があります。それが何がというと…
角度が同じであること!
図から角Aは同じ(対頂角)
角B=角D
角C=角E
このように、角度が同じ点が同じ並びにきていることがわかるかな?(Aが最初、B,Dが2番目、C,Eが3番目)
だから△ABC∽△ADEとかくんだよ。
次に本題の相似比についてだね。
△ABC:△ADE=3:5か2:5かどっちかわかるかな?
相似比とは対応している1組の辺の比のこと。
→対応している1組の辺の見つけ方がわかればOK!
ここで大事になるのが△ABCや△ADEの点の並び順。
△ABC∽△ADE、辺ABに対応するのは辺ADだから
相似比はAB:AD=3:5
規則がわかったかな…?

△ABC∽△ADE
辺BCと対応するのは辺DE
△ABC∽△ADE
辺CAと対応するのは辺EA
これであってるかな?

練習問題
次の図の□の値を求めてみましょう。
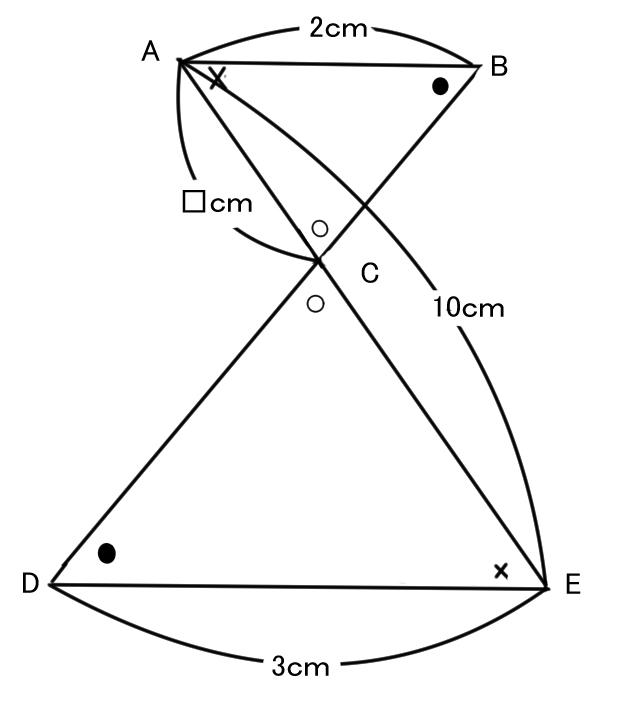

解説)
まず角度が同じ点の通りにかくと
△ABC∽△EDC
1.相似比をみつける
△ABC∽△EDC
AB:ED=2:3
2.相似比を図にかきこむ
△ABC∽△EDC
CA:CE=②:③
3.長さを求める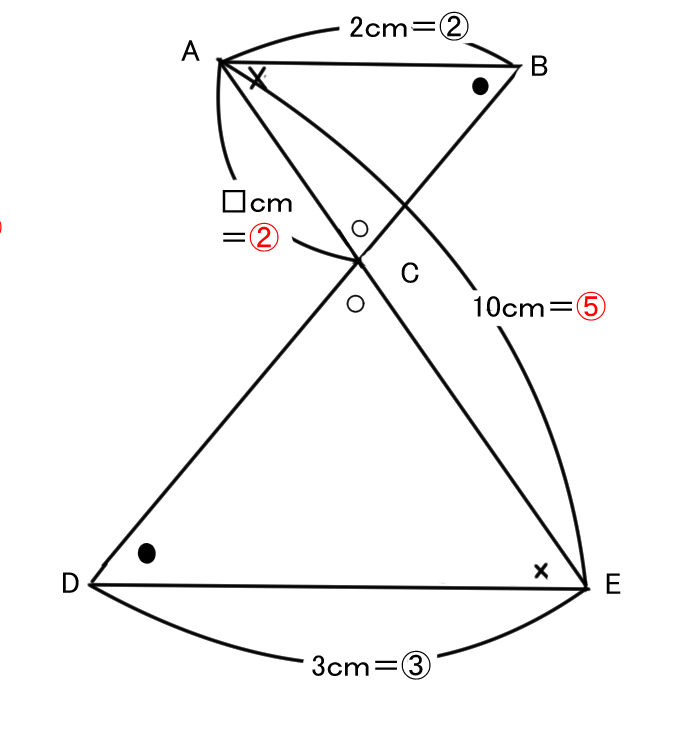
図から②+③=⑤=10cm
①=10÷⑤=2cm
□=CA=②=2×2=4cm
すらすらできた!

今日の目標(解説)
問題
図の□の長さを求めてみよう。


解説)
まず△ABC∽△ADE
1.相似比を見つける
△ABC∽△ADE
BC:DE=4:7
2.図に相似比をかきこむ
△ABC∽△ADE
AC:AE=④:⑦
3.実際に長さを求める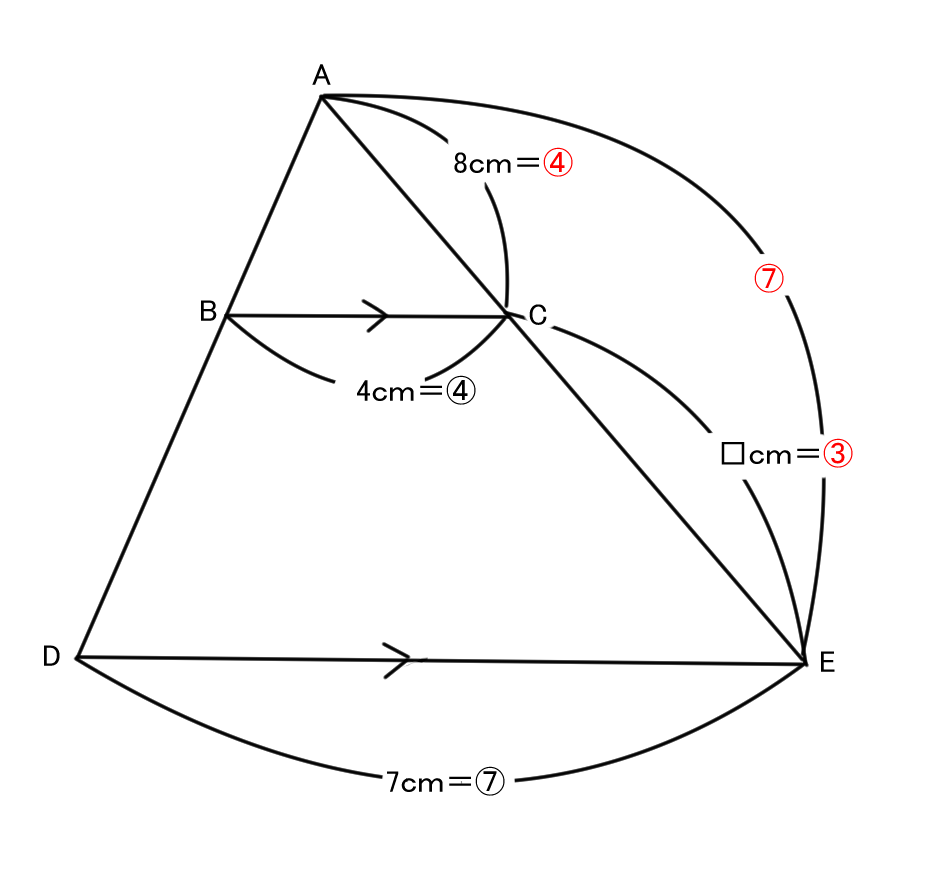
AC=④=8cm
①=8÷④=2cm
図から
□=CE=AE-AC=⑦-④=③
□=③=2×3=6cm
おわり!みんなもわかったかな?
20日目おわり



だけど今日やったことができたらあとは少し手順が増えるだけだから全然大丈夫だよ!ということで今日やったことをおさらいしとこうね。

★ポイント
●相似の三角形を文字で表すときは文字の順番に注意!
(角度の大きさが等しい点が同じ順番になるようにする)
解き方
1.相似比をみつける
2.図に相似比をかきこむ
3.長さを求める
△ABC∽△DEF←これがかけたら辺の比を間違えないようになるからすっごく大事!
これで相似の基本はばっちりだよ。

